If you are new to Computer Science or programming, or if you have started learning Data-Structure and Algorithms, there is a high chance that you have been introduced to the term Big O Notation. As a programmer, it is essential to learn Big O if you want to write optimized code. However, most resources found on the internet teach this topic in a way that is not beginner-friendly.
In this article, I will explain time complexity using Big O Notation in the easiest possible way.
NOTE: I will use JavaScript to show code examples in this article. However, it won't be a problem if you are not familiar with JavaScript, as I will use easy and simple codes that you will understand easily even if you are not from a JavaScript background.
What is Big O?
If you have solved any coding problem previously, you possibly know that in most cases, a single problem can be solved any many different ways. But how can we know which one is the better code for us? Wait! What do I mean by 'Better Code'? Is it the most beautiful-looking code or the code with the minimum lines in it?
No, these are not the way to define the Better Code. Though we can count code readability as one of the qualities of good code, two more important qualities are:
Which code takes less time to execute (known as Time complexity).
Which code consumes less space in our computer's memory (known as Space complexity).
In simple words, Big O is the mathematical representation of the time and space complexity of an algorithm.
But who cares about it?
At the time of solving your school assignment problems or solving random problems from the internet, you may not find it important but when you will be coding for a big organization with millions or billions of users, then you will understand the importance of writing optimized code. But before that, you have to crack an interview. Well, interviewers do care about it so much!!!
So long story short, eventually you have to master optimizing your code and to achieve that, you have to understand the concept of Big O Notation.
The Time Complexity
Let me start with an example to make it easy for you. Let's assume we have to get the sum of all integers up to a number n. We can solve this problem in many different methods, such as:
Method 1: Here we will take a variable sum with value 0 and then add every number starting from 1 to this variable by looping through 1 to n.
function sumUptoN(n) {
let sum = 0;
for (let i = 1; i <= n; i++) {
sum += i;
}
return sum;
}
In this example, we are executing many different operations. Let's visualize this with this image:

So, we are executing (5n + 2) numbers of operations here.
Method 2: Here we will use a mathematical formula that will return the same output but with a different approach.
function sumUptoN(n) {
return (n * (n + 1)) / 2;
}
In this method, we are executing a total of three different operations (one multiplication, one addition, and one division), which is much less than the previous method.
Now let's see the graph of the time complexity of these two methods:
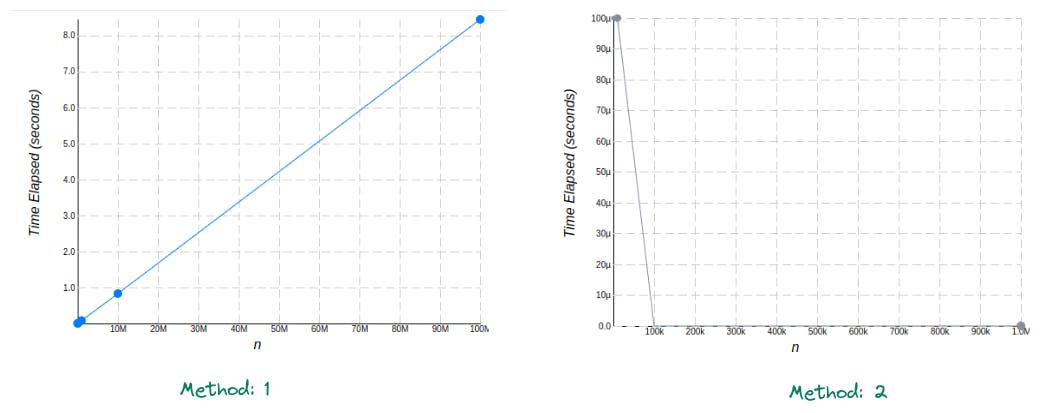
If we analyze the trend of these two graphs, in the first method time is gradually increasing with the increase in the value of n. However, in the second case, time is not dependent on the value of n and it is nearly zero even when n's value is 10 Million while in method 1 it was more than 8 sec at the same value.
By examining the graphs, we can conclude that in method 1, the time required for the computation is almost proportional to the increase in the value of n. Although mathematically more than n number of operations are executed, we only consider the trend that the computation follows while calculating the time complexity, and ignore other constants. Therefore, in Method 1, the time complexity can be represented as O(n). In contrast, Method 2 is not dependent on the value of n, as only three operations are executed at any value of n. As a result, the time complexity is constant, regardless of the value of n. Although the value of the constant is 3, we disregard this specific value and focus on the trend that the computation follows. Hence, we can denote the time complexity of Method 2 as O(1).
Some of the most common Big O expressions are : O(1), O(n), O(n<sup>2</sup>), O(log n), O(n log n). The below Time vs. n graph denotes which Big O expression takes more time to execute and which is more optimized.
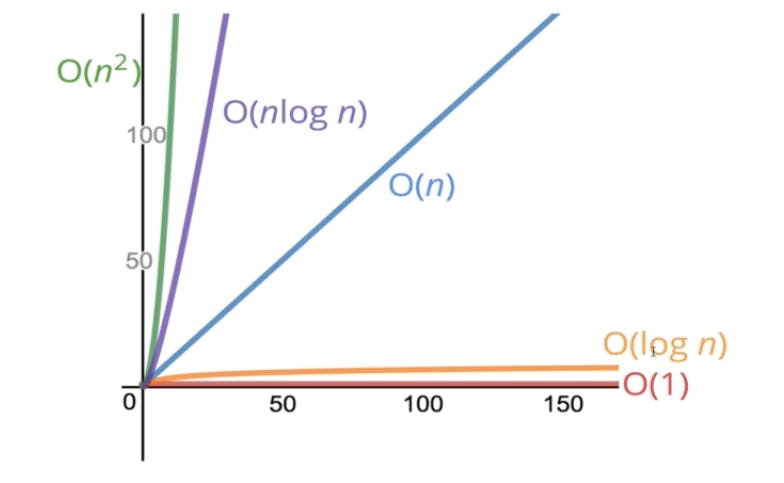
We have already seen examples of O(1) and O(n) time complexity so here we will see examples of the rest of the three complexities.
Ex. 1) Here is a code that prints all the possible combinations between two numbers from 1 to 5.
for (let i = 1; i <= 5; i++) {
for (let j = 1; j <= 5; j++) {
console.log(i, j);
}
}
This code consists of two nested loops. The outer loop iterates from 1 to 5 and the inner loop iterates from 1 to 5 for each iteration of the outer loop.
So, the inner loop will run 5 times for every iteration of the outer loop, giving a total of 5 * 5 = 25 iterations in total.
Therefore, the time complexity of this code is O(n^2), where n is the number of iterations of the outer loop. In this case, n is equal to 5.
As the size of the input increases, the number of iterations increases exponentially, resulting in quadratic time complexity.
Ex. 2) The below code takes an input n and uses a while loop to double the value of i on each iteration until the value of i exceeds n.
function doubleValue(n) {
let i = 1;
while (i < n) {
i = i * 2;
}
return i;
}
Here the while loop doubles the value of ieach time it runs, so it will run log base 2 of n times. This means that the time it takes to run the function grows logarithmically with the size of n. So the time complexity here is log n.
Ex. 3) In the next example a function logArrayElements is defined that takes an array as an argument. The function then loops through the array using a for loop and logs each element of the array along with another element of the array. The second element is determined by another for loop that starts at 1 and doubles its value each time it runs until it is greater than or equal to the length of the array.
function logArrayElements(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 1; j < array.length; j = j * 2) {
console.log(array[i] + " " + array[j]);
}
}
}
In this example, the outer loop runs n times, where n is the length of the array. The inner loop runs log n times for each iteration of the outer loop. This is because j starts at 1 and doubles each time until it is greater than or equal to n. Since log base 2 of n is the number of times you can double 1 until you reach n, the inner loop runs log n times. So the time complexity here is O(n log n).
Wrapping up!
In conclusion, Big O notation is a vital concept that every programmer should learn to write optimized code. Throughout this article, we have simplified the explanation of time complexity using Big O notation, providing numerous examples to help solidify your understanding. We have covered essential notations such as O(1), O(n), O(n^2), O(log n), and O(n log n) while noting that other notations also exist for determining the time complexity of an algorithm. We intentionally focused on beginner-friendly notation to ensure that this article serves as an accessible introduction to the topic. With this knowledge, you can now analyze and optimize the efficiency of your code with confidence.

